树¶

树通常用来存储和组织具有层级结构的数据，比如磁盘驱动器上的文件系统，还常用来组织数据，让集合能够快速查找、插入和删除，以及作为网络路由算法等等。

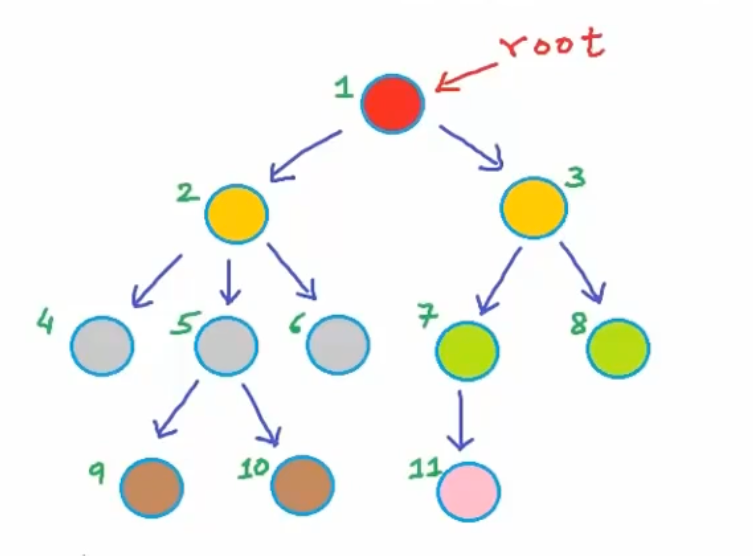
树是从上至下由节点(node)和边(edge)组成的，树的节点包含一些数据，可以是任何类型

如果可以从节点 A 到节点 B，则 A 被称作 B 的祖先(ancestor)，B 是 A 的子孙(descendent)

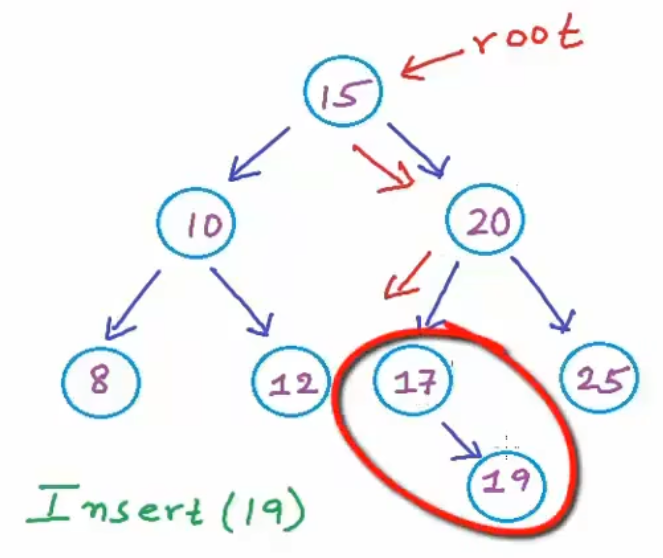
如图，1、2、5 都可以称作 10 的祖先，4、9 的共同祖先是 1、2

没有祖先的顶部节点，称做「根节点 root」，至少有一个子节点被称为「内部节点」，没有子孙节点则被称作「叶子节点 leaf」

1 是 2、3 的「父节点 parent」，2、3 是 1 的「子节点 children」，2 是 9、10 的祖父节点

同一父节点下的子节点之间互为「兄弟节点 sibling」，比如 4、5、6，而 6、7 拥有相同的祖父节点，只能称作堂兄节点，3 可以叫做 6 的叔节点

树的属性¶

不难发现，树是一种递归结构，在实现和使用树的过程中，递归属性随处可见

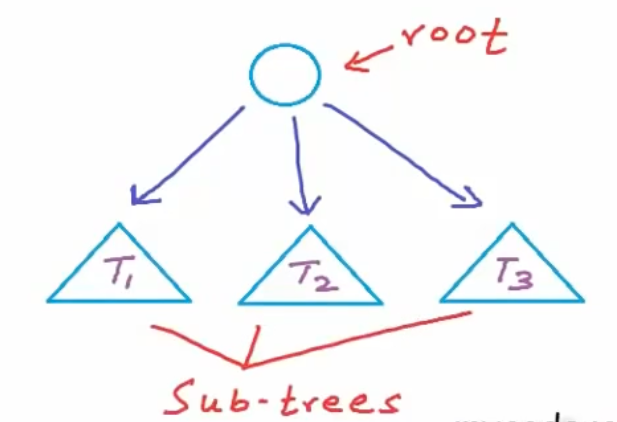
树由根节点和子树递归组成，根节点包含指向所有子树根节点的链接

除了根节点，所有节点都只有一个指向它的边，因此，在一个有效的树中，如果有 N 个节点，就会有 \(N - 1\) 条边

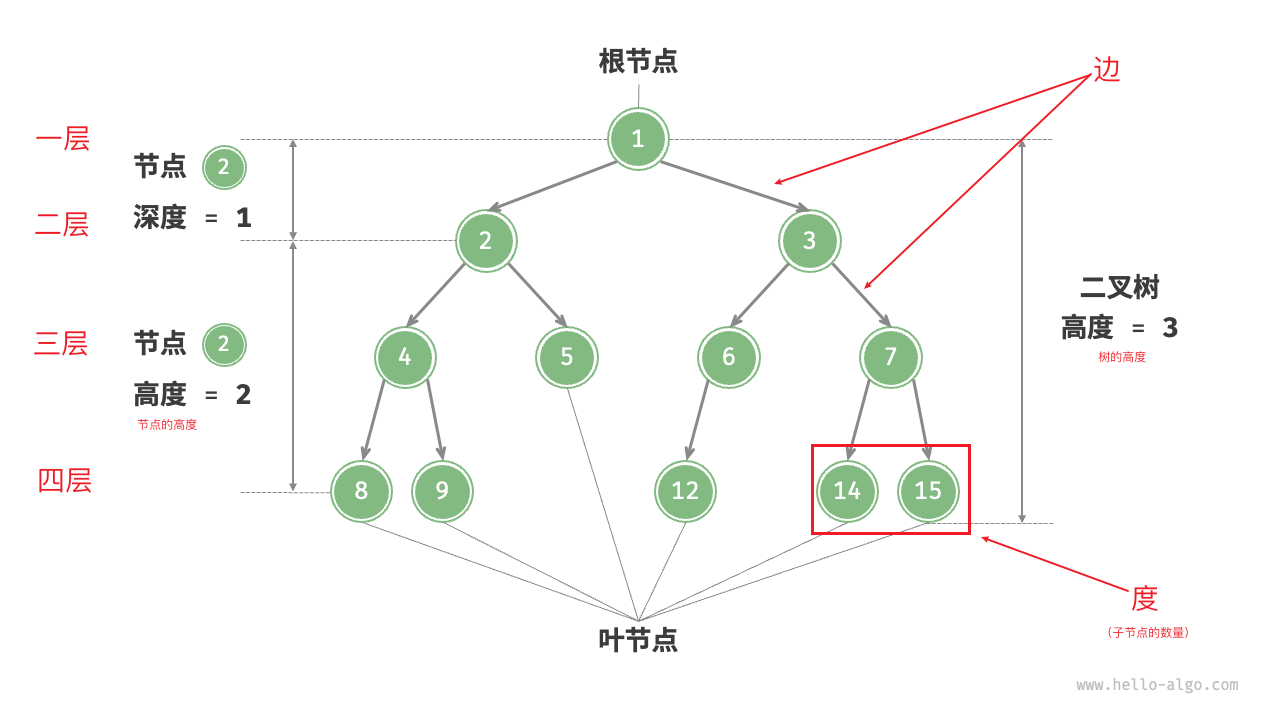
度：子节点的数量

深度：根节点到目标节点的路径上包含的边数，下图节点 5 的深度为 2

高度：从目标节点到任意叶子节点的最长路径的边数，所以下图

根节点的高度为 3
节点 3 的高度为 2
叶子节点的高度是 0

根节点的高度也被称为「树的高度」，即从根节点到叶子节点的最长路径的边数

所以只有一个节点的树的高度是 0，而没有节点的（被称为空树）高度是 -1

另一种关于高度的非常规定义是指节点的数量，即只有根节点的高度是 1，空树的高度是 0

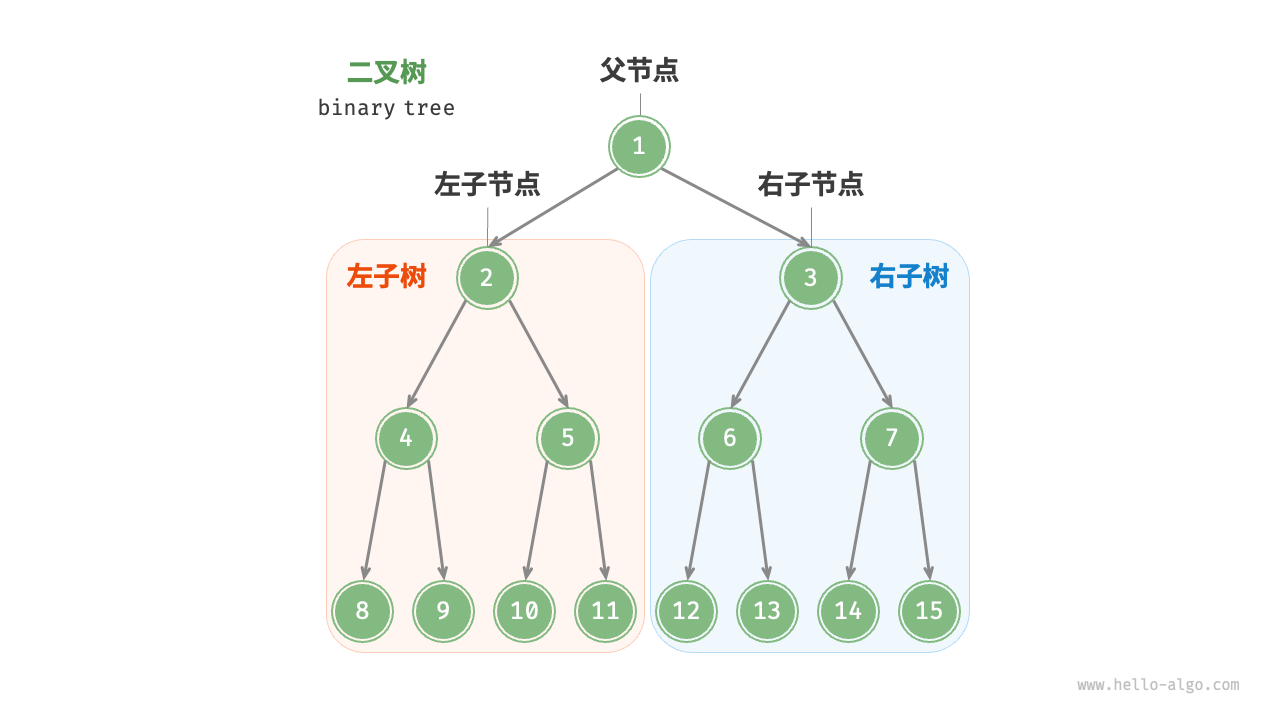
二叉树¶

只要节点的子树不超过两个，都是二叉树（Binary Tree）

比如：有两颗子树；只有左子树或右子树；没有子树（只有根节点）

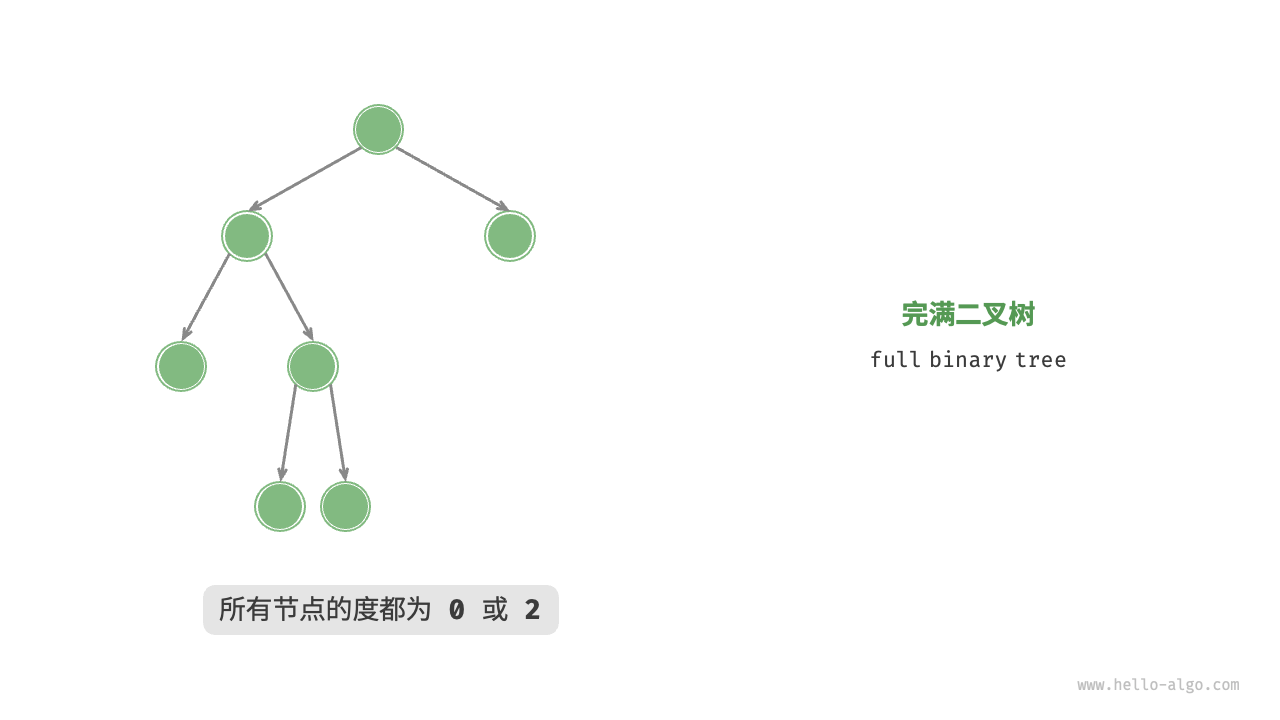
完满二叉树（严格二叉树）：每个节点都有 2 或 0 个子节点

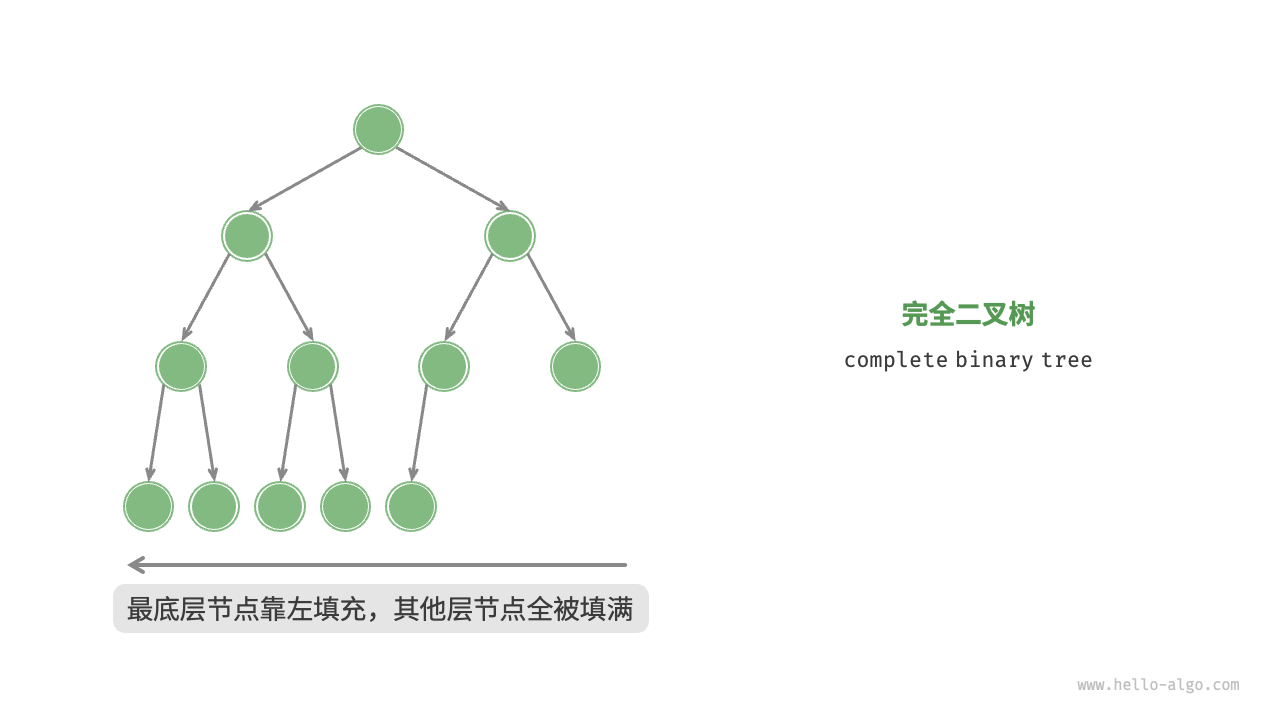
完全二叉树：除最底层外，其它层节点都填满（节点填满，而不是说要有子节点），且最底层节点都靠左对齐

注意，这不是一个完全二叉树，需要给 5 加一个左子节点才算连续

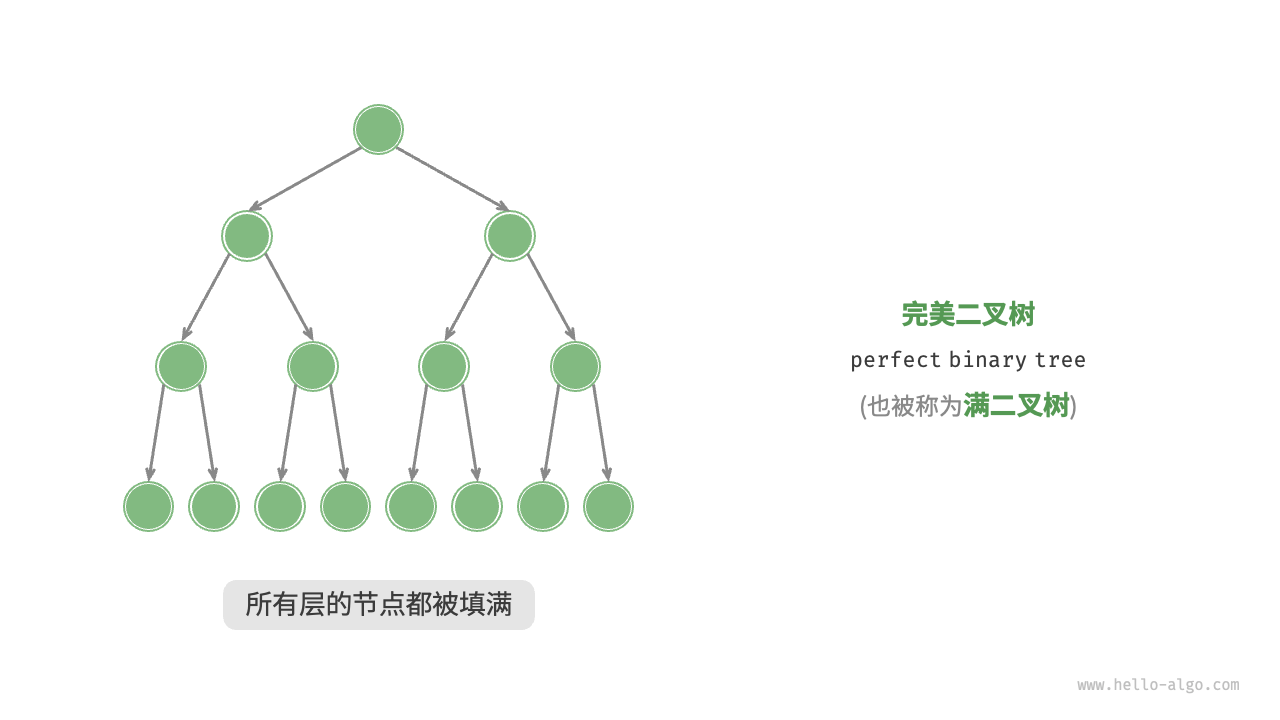
完美二叉树（满二叉树）：所有层节点都填满
- 每层节点数为：\(2^i\)（i 表示层数）
- 节点总数为 \(2^{h+1} - 1\)（h 表示树的高度）
- 节点数为 n 的完美二叉树的高度为 \(log_2(n+1) - 1\)

时间复杂度¶

二叉树不同操作（搜索、插入、删除）的复杂度，与树的高度成正比

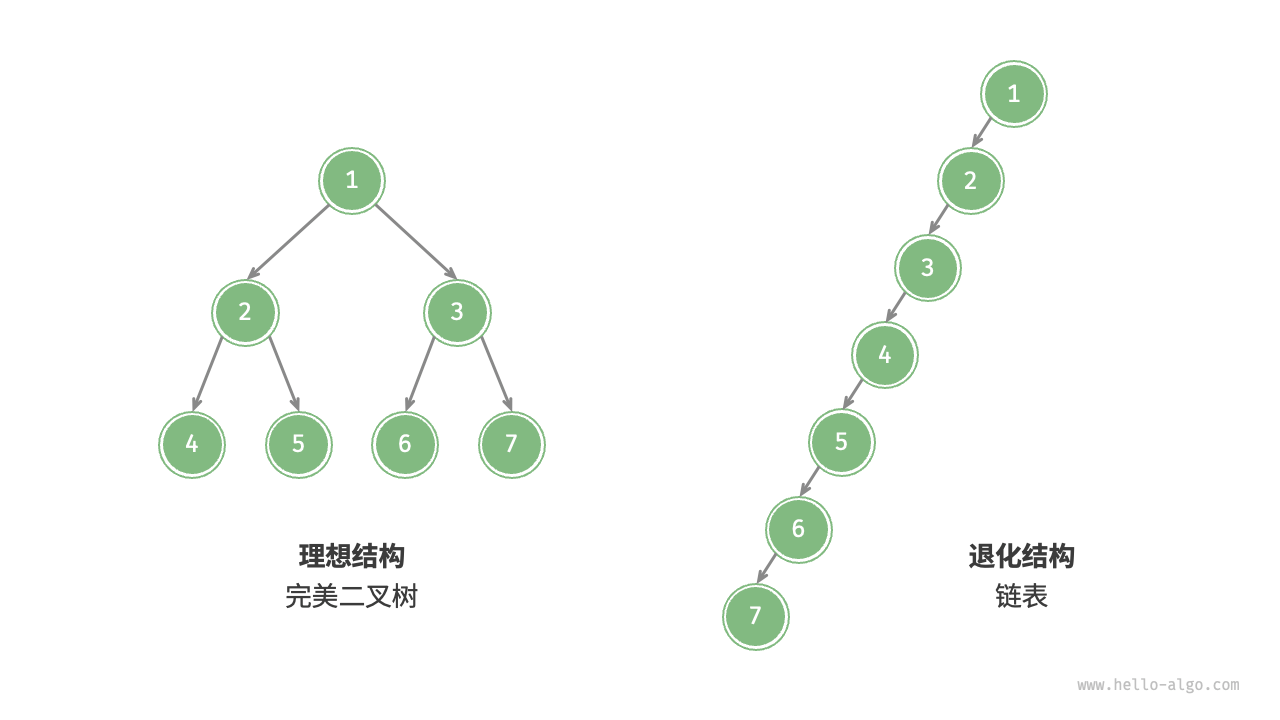
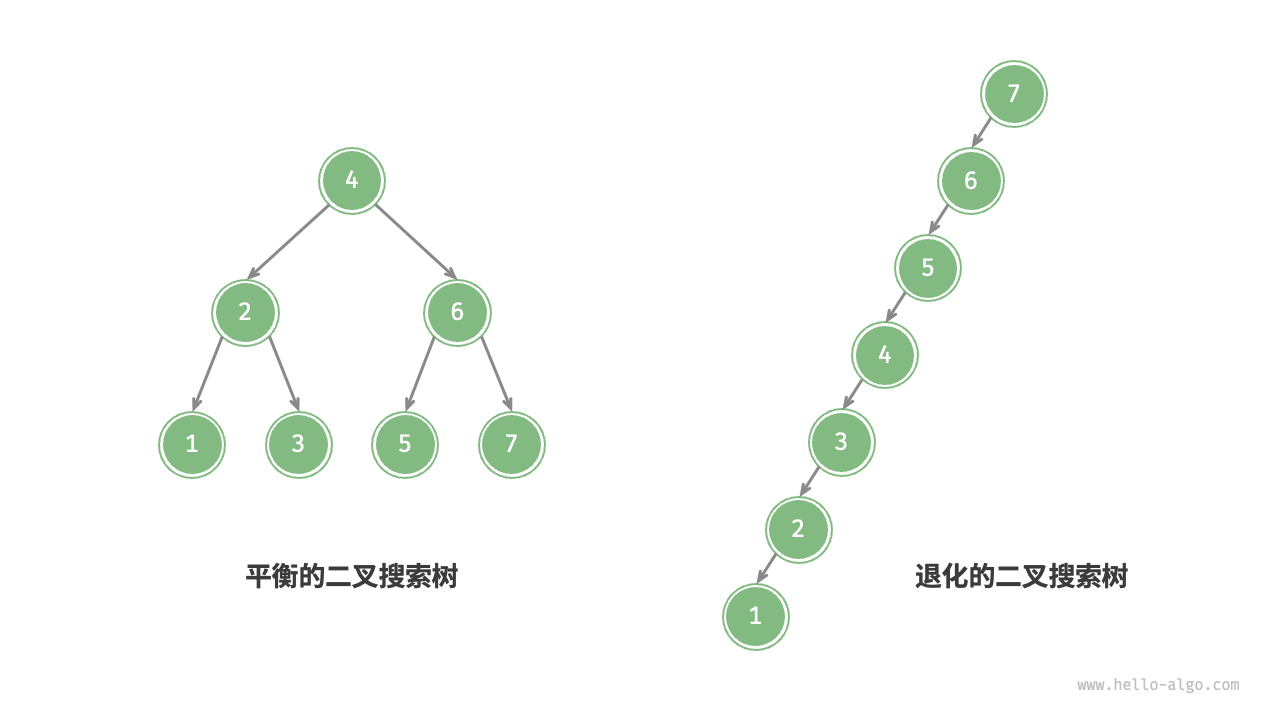
二叉树的最佳结构，就是完美二叉树，最差结构，是所有节点都偏向一侧，即退化为了链表

也就是说，节点数为 n 时，二叉树的高度 h 范围为：\(log_2(n+1) - 1\) ~ \(n-1\)

即时间复杂度范围 \(O(h)\) 为：\(O(log_2n)\) ~ \(O(n)\)，假设 n 为 \(2^{100}\)，则范围为：\(100\) ～ \(2^{100}\)

所以我们要尽可能降低树的高度，换言之，就是让二叉树尽量保持平衡

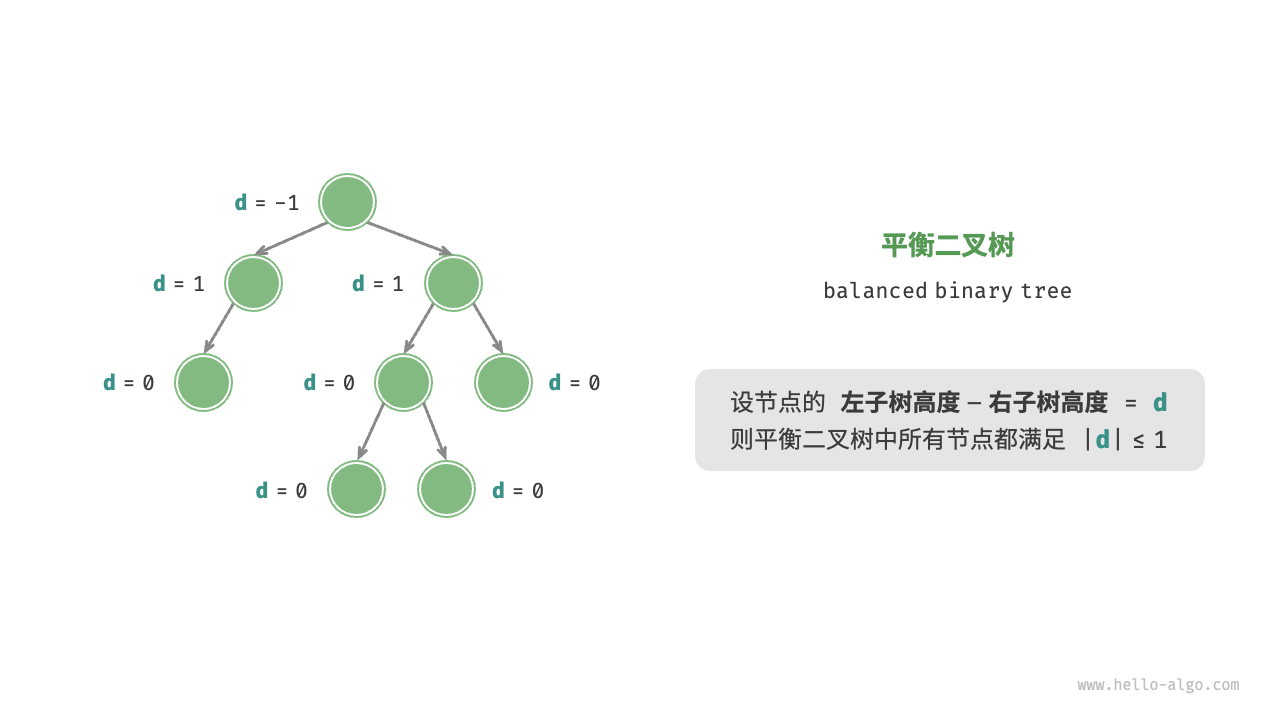
所谓的平衡二叉树，是指任意节点左右子树的高度差不超过 1，即 \(|d|<1\)（-1、0、1）

如上图，第二层左边节点，左子树只有一个节点，所以高度为 0，右子树为空，所以高度为 -1，则高度差 \(diff = |0 - (-1)| = 1\)

遍历¶

遍历（Traversal）方式是通过指针逐个访问节点，但由于非线性，遍历树要更复杂，需要借助搜索算法。

广度优先遍历（Breadth-First, BFS）：层序遍历（Level-order）

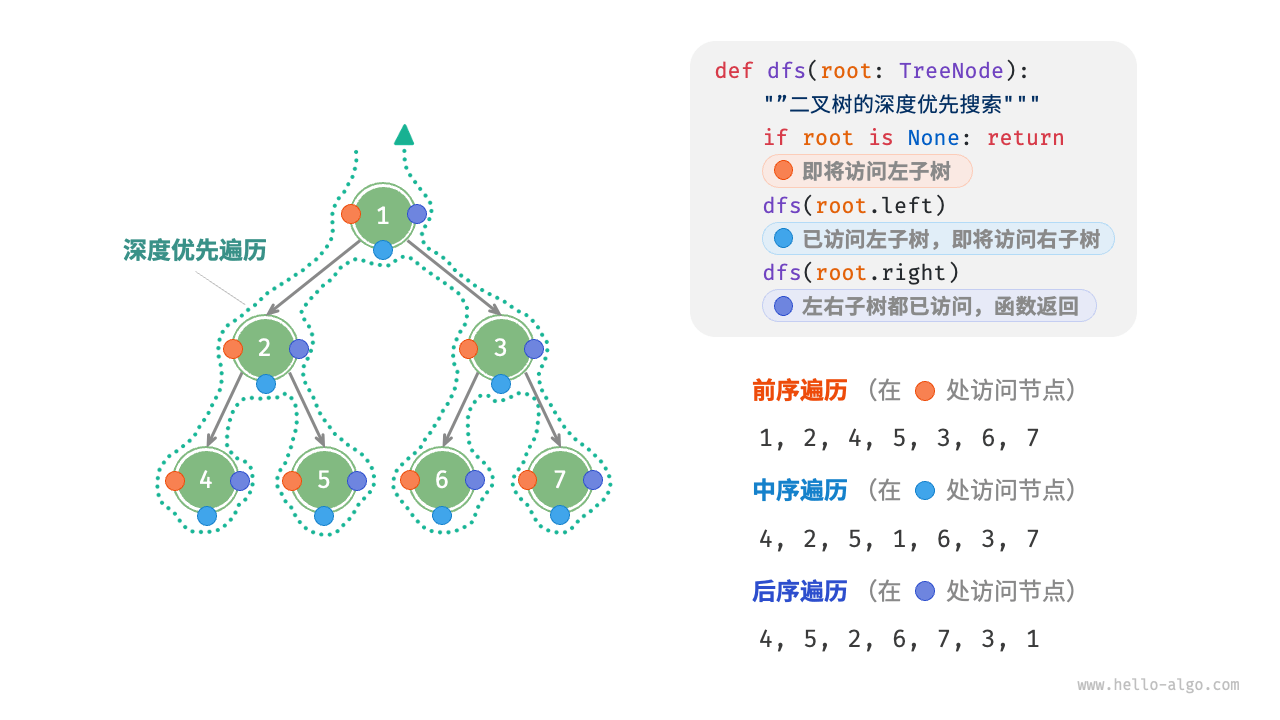
深度优先遍历（Depth-First, DFS）：根据 root 节点（存储的是数据 Data）被访问的顺序可以分为
- 前序遍历（Pre-order）：root -> left -> right，即 DLR
- 中序遍历（In-order）：left -> root -> right，即 LDR
- 后序遍历（Post-order）：left -> right -> root，即 LRD

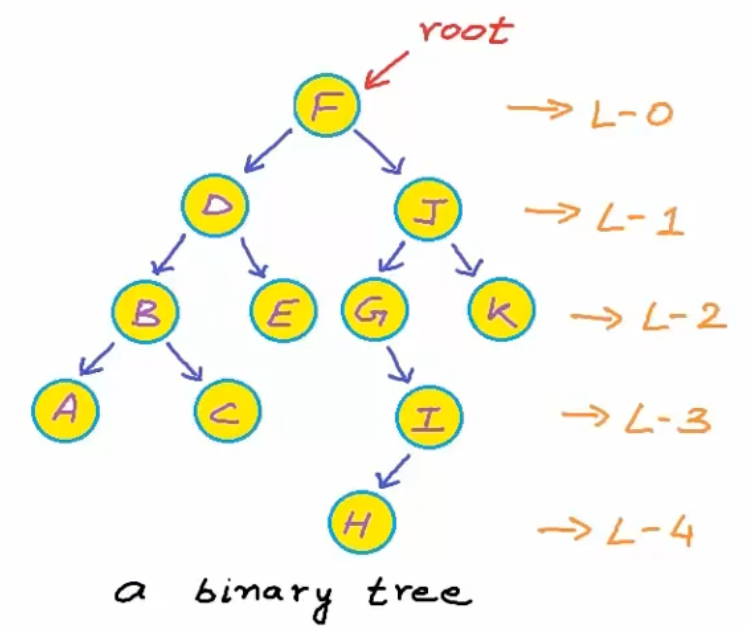
如图所示的二叉搜索树

层序遍历：F, D, J, B, E, G, K, A, C, I, H
前序遍历：F, D, B, A, C, E, J, G, I, H, K
中序遍历：A, B, C, D, E, F, G, H, I, J, K
后序遍历：A, C, B, E, D, H, I, G, K, J, F

二叉搜索树，使用中序遍历，会得到一个从小到大的有序列表

底层存储¶

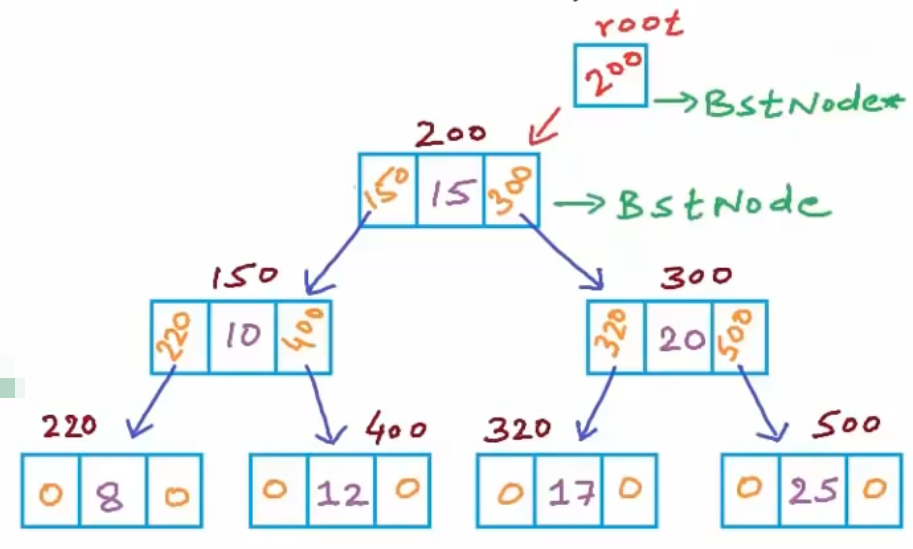
从物理结构来看，树是一种基于链表的数据结构，可以动态创建节点，使用指针或引用将它们链接起来

与链表类似，在二叉树中插入与删除节点可以通过修改指针来实现。

删除节点可以有两种策略，一种是只删除节点（将其父节点与其子树链接），另一种是删除节点及其子树（父节点引用置为空）。

class TreeNode:
    """二叉树节点类"""
    def __init__(self, val: int):
        self.val: int = val                # 存储节点的值
        self.left: TreeNode | None = None  # 存储左子树根节点的地址
        self.right: TreeNode | None = None # 存储右子树根节点的地址

# 初始化二叉树
n1 = TreeNode(val=1)
n2 = TreeNode(val=2)
n3 = TreeNode(val=3)
n4 = TreeNode(val=4)
n5 = TreeNode(val=5)

# 构建节点之间的引用（指针）
n1.left = n2
n1.right = n3

n2.left = n4
n2.right = n5

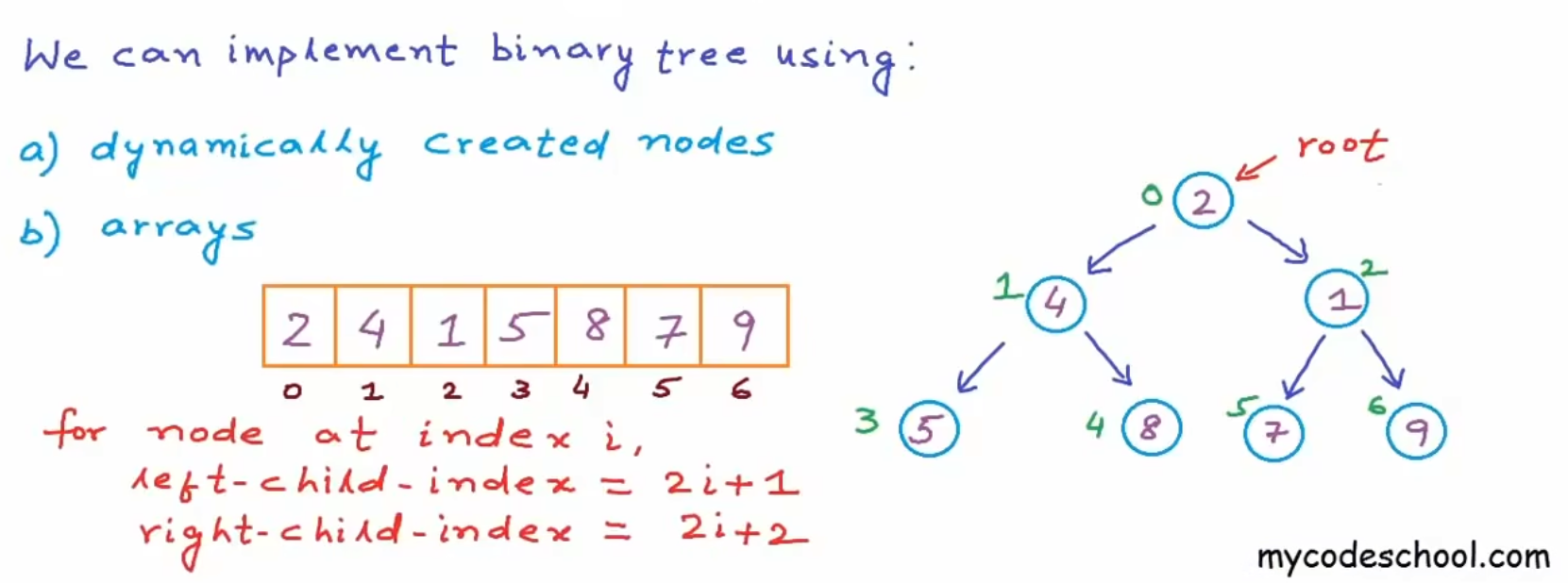
在一些特殊情况下（比如完全二叉树），也可以用数组表示二叉树，将所有节点按照层序遍历的顺序存储在一个数组中，则每个节点都对应唯一的数组索引。

对于完全二叉树来说，节点索引为 \(i\)，则左子树的索引为：\(2i + 1\)，右子树的索引为：\(2i + 2\)，父节点索引为：\((i-1)/2\)

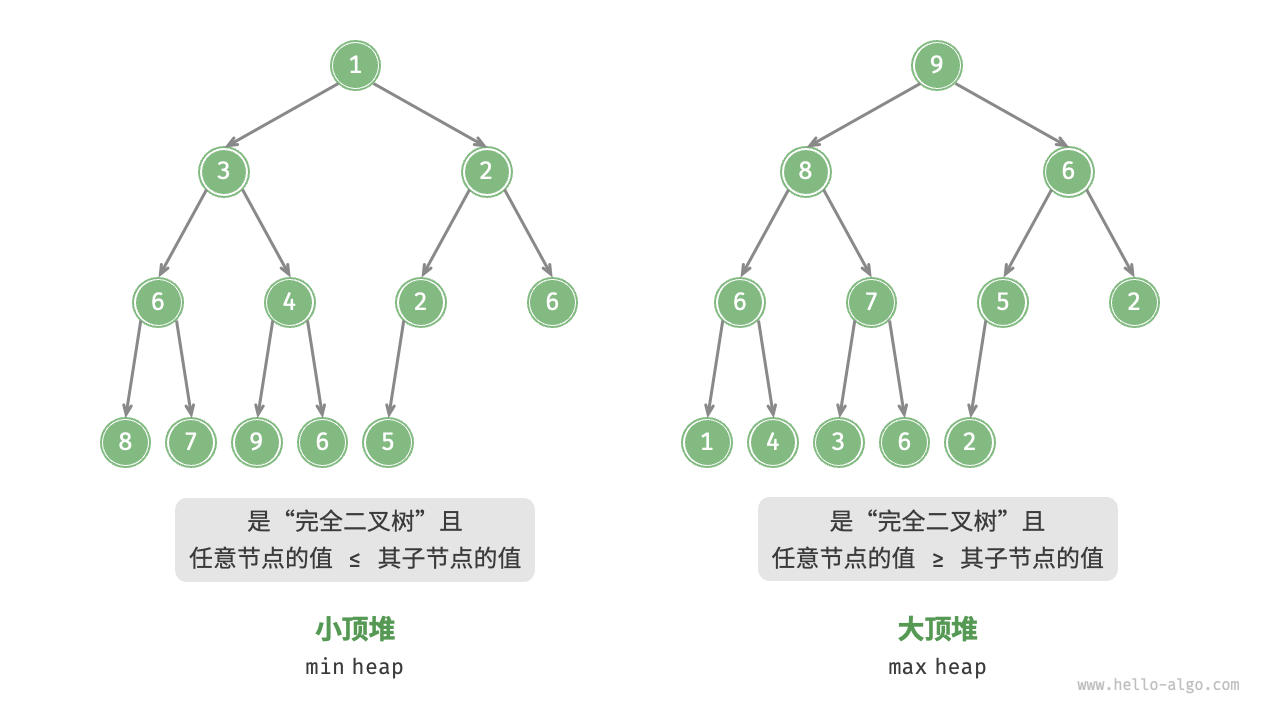
堆¶

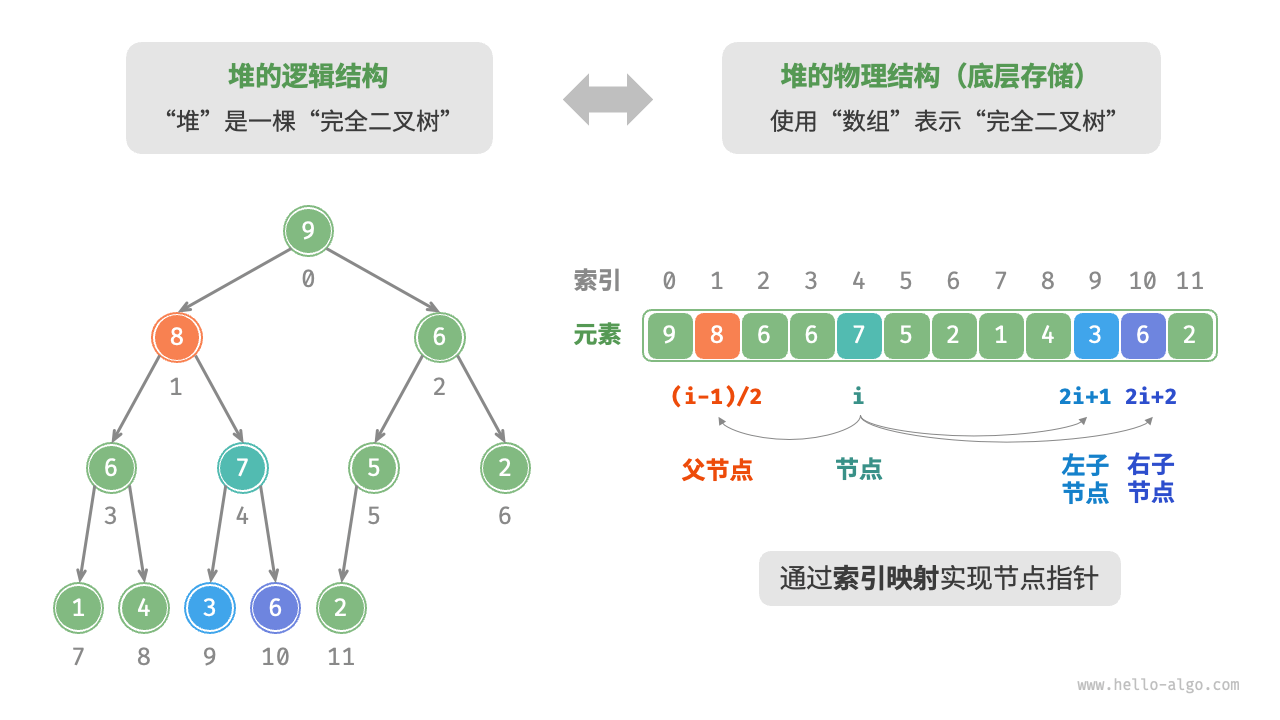
堆（Heap）是一种满足特定条件的「完全二叉树」

所以通常采用数组来存储堆，根节点称为堆顶，将底层最靠右的节点称为堆底

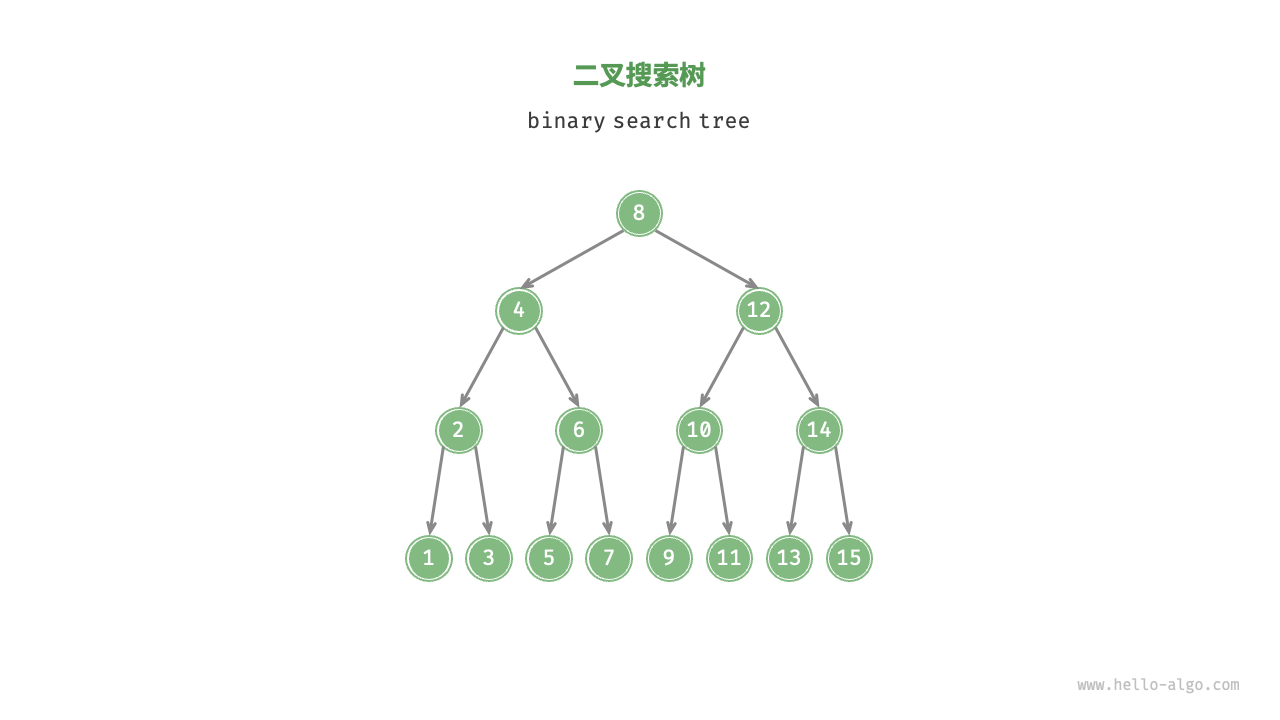
二叉搜索树¶

二叉搜索树（Binary Search Tree, BST），也叫二叉查找树，指的是二叉树中任意节点 左子树各个节点的值 < 根节点值 < 右子树各个节点的值

通常用来组织数据以进行快速搜索和更新，比如系统中的多级索引

对一个集合，进行搜索和更新操作，使用 BST 存储是最高效的（前提是保证平衡）

BST 的搜索类似于二分查找法，先与根节点的指比较，小于根节点，就继续与左子树的根节点继续比较，大于就与右子树根节点比较，直到等于。

BST 的插入，不需要像数组那样移动节点，只需要引用到左子树或右子树中，是一个常数，因此和搜索的复杂度一样

BST 在每次插入或删除节点之后，可能会变得不平衡，所以需要通过算法自动调整（旋转、分裂、合并），以保持树的平衡，从而确保树的高度保持在平衡因子范围内（-1、0、1），这就叫「自平衡」

自平衡二叉搜索树：

AVL 树，自平衡二叉搜索树，且任意节点的两个子树的高度差 < 1
红黑树，自平衡二叉搜索树，且从根到叶子的最长路径 / 最短路径的比值 ≤ 2

多路搜索树¶

B 树（B-Tree）：自平衡多路搜索树，所有的叶子节点都在同一层，主要目的就是减少磁盘的 I/O 操作
B+ 树（B+ Tree）
Trie 树（字典树、前缀树）用来存储字典，非常快速和高效，用于动态拼写检查