Encode¶

编码是将信息从一种形式转换为另一种形式，以便数据表示、兼容性、压缩与加密的过程。

在自然语言中，通常使用十进制(Decimal)，而在芯片内使用的是门电路，只能表示 0 和 1 两个状态，即在计算机中，所有数据都是以二进制数(Binary digit，简称 bit，比特)的形式存储的。

此外还有八进制(Octal)和十六进制(Hexadecimal)等，4bit 可表示一个十六进制数，1Bytes 则表示两个十六进制数。

单位¶

1 bit 在内存中占 1 位，8 位称作 1 个字节(Bytes)

bit，常用于表示数据传输速率，bit/s：bps, bit per second

Byte，常用于表示数据存储大小

千字节 KB = 2^10 = 1024B
兆字节 MB = 1024KB
吉字节 GB
太字节 TB

进制转换¶

与十进制互转¶

其它进制转十进制：系数*基数^权次幂

系数从1开始递增，几进制基数就是几，权从0开始递增

十进制，满10进1，基数为10
0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15...
1024 = 1*10^3+0*10^2+2*10^1+4*10^0 = 1*1000+0*100+2*10+4*1 = 1024
数位为: 10^(n-1), ..., 1000, 100, 10, 1

二进制，满2进1，基数为2
0,1,10,11,100,101,110,111...
0b110 = 1*2^2+1*2^1+0*2^0 = 1*4+1*2+0*1 = 6
数位为: 2^(n-1), ..., 16, 8, 4, 2, 1

八进制，满8进1，基数为8
0,1,2,3,4,5,6,7,10,11,12,13,14,15...
0o711 = 7*8^2+1*8^1+1*8^0 = 7*64+1*8+1*1 = 457
数位为: 8^(n-1), ..., 512, 64, 8, 1

十六进制，满16进1，基数为16
0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F,10,11...
0xABC = 10*16^2+11*16^1+12*16^0 = 10*256+11*16+12*1 = 2748
数位为: 16^(n-1), ..., 4096, 256, 16, 1

int(0b1111)  # 15
int(0o17)  # 15
int(0xf)  # 15

十进制整数转其它进制：除基取余倒序，直到商为0

几进制基就是几

bin(15)  # 转成二进制 0b1111
oct(15)  # 转成八进制 0o17
hex(15)  # 转成十六进制 0xf

十进制小数转其二进制：乘基取整正序

# 比如 3.26 转换为二进制
"""
整数部分：11
小数部分：
0.26 * 2 = 0.52
0.52 * 2 = 1.04
1.04 * 2 = 0.08
0.08 * 2 = 0.16
0.16 * 2 = 0.32
0.32 * 2 = 0.64
0.64 * 2 = 1.12

最终得到：11.0100001
"""

def float_to_binary(num, precision):
    if num < 0 or num >= 1:
        return "num need in 0~1"

    binary = "0."
    while precision > 0:
        num *= 2
        if num >= 1:
            binary += '1'
            num -= 1
        else:
            binary += '0'
        precision -= 1
    return binary

# 示例：将0.26转换为二进制，精度为7位
float_to_binary(0.26, 7)  # 0.0100001

不难发现，浮点数的小数如果不是0或者5结尾，将无法准确的转为二进制，只能得到某个精度的近似值。

比如 0.1
转为二进制将变成一个无限循环小数：0.00011001100110011...
再加上有限精度，存储时取近似值，计算结果再转为十进制必将是不准确的

因此各种编程语言以及数据库中的浮点数类型计算都是不精确的，对精度要求较高的业务场景通常使用定点数DECIMAL将整数和小数部分拆分开来存储。

与二进制互转¶

快速计算：8421 码

其它进制转二进制

bin(13)  # 0b1101
bin(0o15)  # 0b1101
bin(0xd)  # 0b1101

二进制转其它进制

int(0b1101)  # 十进制，无需分组，13
oct(0b1101)  # 八进制，3位一组，0o15
hex(0b1101)  # 十六进制，4位一组，0xd

数字编码¶

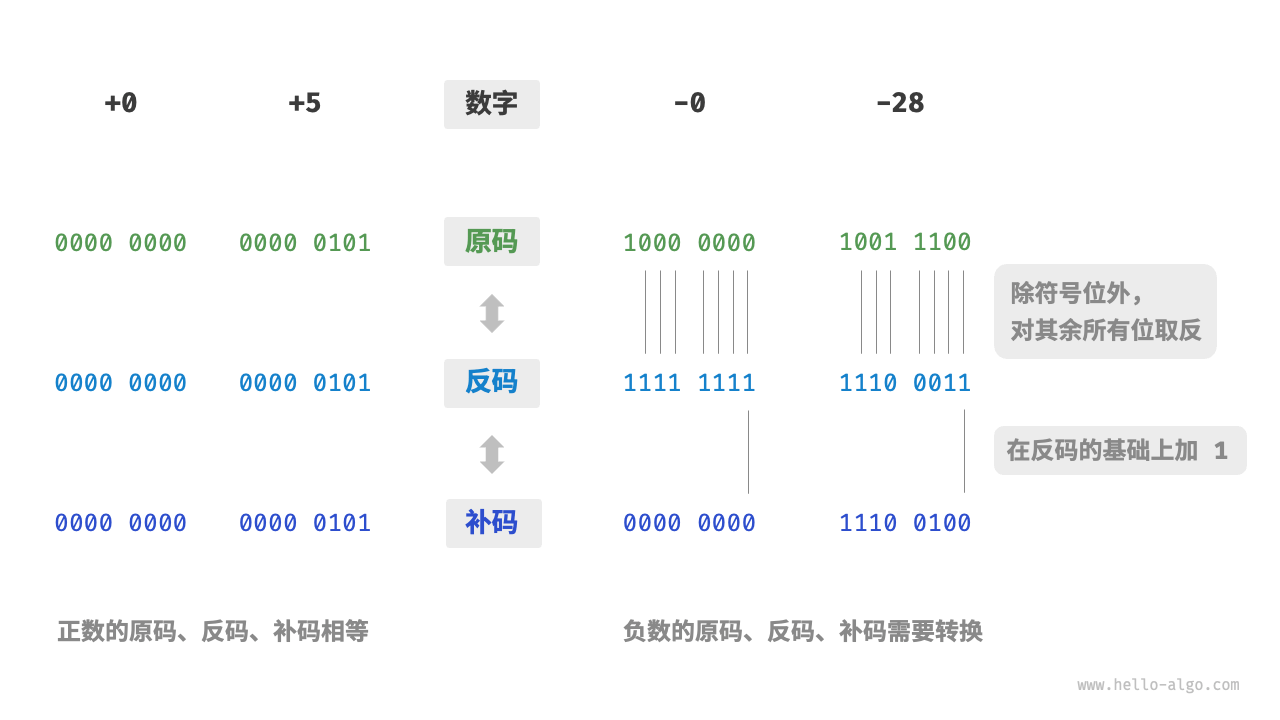
数字的二进制表示有三种形式

原码 sign-magnitude：最高位视作符号位，0 表示正数，1表示负数，其它位表示值
反码 1's complement：正数的反码与原码一致，负数的反码是将数值位取反
补码 2's complement：正数的补码与原码一致，负数的补码是在反码的基础上加1

数字是以补码的形式存储在计算机中的，之所以如此设计，是因为正数与负数的原码相加是错误的，而反码与原码的0存在正负之分，而负0的补码与正0的补码相同，都是 0000 0000，所以在补码中0不会产生歧义。

正因如此，各种运算都可以基于加法实现，以此精简计算机的电路设计，比如，计算减法 a - b 可以转换为计算加法：a + (-b)，计算乘法和除法可以转换为计算多次加法或减法。

整数¶

1Bytes = 8Bit，最高位表示符号，剩余 7 Bit 可以表示 2^7=128 个数：0～127，算上符号就是：[-127, 127]

原码：1111 1111 ～ 0111 111
反码：1000 0000 ～ 0111 111
补码：1000 0001 ～ 0111 111

不难发现，补码 1000 0000 没有对应的原码，于是便规定它表示 -128，所以 1Bytes 可表示的范围实际为：[-128, 127]

-127 + -1
原码：1111 1111 + 1000 0001
反码：1000 0000 + 1111 1110
补码：1000 0001 + 1111 1111 = 1000 0000
由于1字节只有8bit，所以进位溢出舍弃，最终得到的补码恰好为 -128

浮点数¶

十进制的浮点数由整数和小数组成

二进制的浮点数由三部分组成

符号位（Sign Bit）

0表示正数，1表示负数

分数位（Fraction）

也叫尾数位（Mantissa），表示浮点数的小数部分，单精度有23bit，双精度有52bit

取值范围为：[1, 2-2^-23]

指数位（Exponent）

也叫阶码，决定了浮点数的数量级，单精度有8bit，双精度有11bit

为了能够存储正负指数，以及消除正负0的歧义，指数部分通常需要加上一个固定的偏移值，在 IEEE 754 标准中，单精度偏移值是 2^(8-1) - 1 = 127，双精度是 1023。

因此存储的二进制浮点数转十进制时，指数位需要减去偏移值

指数位的取值范围应该有 2^8=256 个：[0, 255]，但 0 和 255有特殊含义

正规数的小数部分以1开头，最大的正正规数为：2^(254 - 127) * (2 - 2^-23) ≈ 3.4 * 10^38，最小正正规数为：2^-126

次正规数的小数以0开头，用于表示0和最小正规数之间的小数，最小正次正规数为：2^-126*2^-23

比如 13.75

整数部分的 13，转为二进制 1101
小数部分的 0.75 转为二进制 0.11
合起来为：1101.11
科学计数法表示为：1.10111x2^3

存储为单精度浮点数形式为
符号位：为正数，用 0 表示
指数部分（用偏移值表示）：3+127=130，转为8位二进制 10000010
尾数部分（补充到23位）：10111000000000000000000
合起来后就是：0 10000010 10111000000000000000000

字符编码¶

为了用二进制表示字符，需要建立一套字符集，让字符与二进制数之间产生对应关系

ASCII¶

由于计算机诞生于美国，所以最早的美国标准信息交换代码 ASCII（American Standard Code for Information Interchange）编码系统只考虑了大小写英文，0～9、一些标点符号以及控制字符，使用了 0～127 共 128 个整数，只需要 7bit。

ASCII 字符表前32个字符都是控制字符，很多都源于遥远的电报时代，比如，当电传打字机打印完一行之后，需要用一个控制命令把打印头复位回打印纸的左边，然后再用另一个控制命令把打印头往下移动一行，这俩动作分别对应了两个控制字符（CR ＆ LF），也就是所谓的回车和换行

后来计算机传入西欧，他们所特有的字符无法完全用 ASCII 表示，于是增加了表格符号，计算符号，希腊字母，拉丁符号等扩展到了 8bit，统称 EASCII

Unicode¶

无论 ASCII 还是 EASCII，使用 1 字节即可表示，所以属于单字节系统。

但是汉字有成千上万个，即使常用的也有 2500 个，所以至少需要两个字节来表示，于是中国在 ASCII 的基础上制定了 GB2312 编码（包含 6763 个汉字），后来又在此基础上创建了GBK（27484 个汉字，同时还包含藏文蒙文维吾尔文等少数民族文字），除了中国外，还有其他国家也会存在这样的问题，比如日文，韩文等，每个国家都制定一套自己标准，不可避免的会出现冲突。

于是人们就想着把所有语言统一到一套编码中，当时做这件事的有两个团队，一个叫 UCS，一个叫 Unicode，当他们发现对方的存在时决定共同搞一套规范，名字就叫 Unicode，俗称万国码，或统一码。它也是兼容 ASCII 的。通常用 U+xxx 形式表示。需要被定义的符合有很多，所以它肯定不是一次性定义完的，比如7.0版本时已收录了 10w+ 符号，那它是咋定义的呢：分区，每个区可以存放 2^16 个字符，被称为一个平面，目前共有 17 分区/平面。最先被定义的肯定是最常见的那些字符，它们被放在了第一个分区/平面，称作基本平面（缩写为 BMP，从 U+0000 到 U+FFFF）剩下的都叫辅助平面（SMP）

UTF-8¶

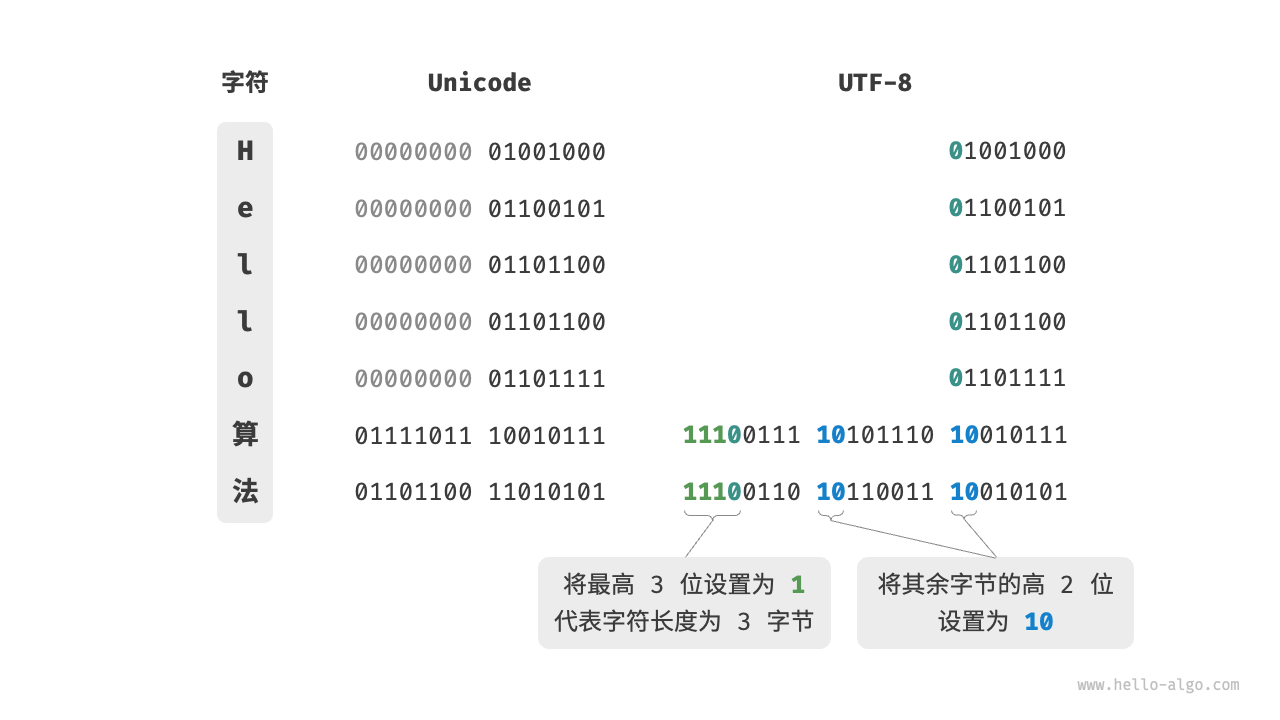
Unicode 只规定了每个字符对应的码点（编号），而一个码点占用几个字节由 Unicode 的编码方式 UTF 规定，也叫字符集，比如 UTF-32，规定 32bit 表示一个码点，但这出现了一个问题，就是如果文本都是纯英文的话，那么就比直接用 ASCII多 4 倍的存储空间。

所以出现了变长型的 UTF-8 编码，它会根据不同码点大小占用 1~6 个字节，比如英语通常为 1 字节，汉字为 3 字节，很节省空间。一般在计算机内存中会统一使用 Unicode，但在存储和传输的时候都会转换为 UTF-8 以节省空间和提高性能。

Python3、Go、Rust 等语言的字符串默认使用 UTF-8，但 Python2 比 Unicode 诞生要早，所以默认编码是 ASCII，一般需要在源码开头声明编码格式

Python3 中用到 utf_8 时可忽略大小写，还可用 _ 替代 -，所以这些别名也都有效：utf-8, utf8, UTF-8, U8, UTF, cp65001，但使用别名可能会导致执行速度变慢

#!/usr/bin/python
# -*- coding: utf-8 -*-
"""
第一行. 告诉类Unix系统这是一个Python可执行程序，Windows系统会忽略这个注释
第二行. 告诉Python解释器按照UTF-8编码读取源代码，也可以写为：coding=utf-8
"""

UTF-16¶

Java、C#、ES6 等使用了 UTF-16，结合了定长和变长的方式。基本平面的字符占用 2 个字节，辅助平面占用 4 个，就是说要么占用 2 个要么 4 个字节。其实 UTF-16 是之前的 UCS-2 的超集，后来取代了 UCS-2，因为 UCS-2 有个问题就是一个字符如果是4字节的会被当成两个 2 字节的字符，而 UTF-16 为此做了一个巧妙的设计（辅助平面的字符被拆成了两个基本平面的字符表示）避免了这个问题。

由于 JS 诞生于（1995年）UCS-2（1990年）和 UTF-16（1996年）之间，所以最初选用了 USC-2 编码方式（没有选用 UTF-8 是因为当时 UTF-8 还不成熟，而UCS-2在内存方面操作及使用效率更高），不过 ES6 已经改为默认 UTF-16，不会再有4字节的问题。

字节流编码¶

用于将二进制数据转换为 ASCII 字符，通常用于只能处理文本数据的系统或协议

URL 参数
在 HTML 或 CSS 文件中嵌入图像或其他二进制文件
JSON 中传输图像或文件
电子邮件协议（如 SMTP）发送和接收

Base64¶

Base64 将二进制数据每三个字节作为一组，共 24 位，然后将这 24 位分成四组，每组 6 位，通过查找 Base64 编码表转换成一个字符，总共产生四个字符。

原始数据的大小越大，转换后的 Base64 字符串长度也越长。

import urllib.parse
import base64

binary_data = b'Sample data'
base64_data = base64.urlsafe_b64encode(binary_data).decode('utf-8')
url = f'https://example.com/data?value={urllib.parse.quote(base64_data)}'
print(url)

假设有一段包含多语言文本的文件，并且需要通过电子邮件发送这段文本。你可以先使用 UTF-8 将文本编码为二进制，然后使用 Base64 将其转换为可传输的文本格式，通过这种方式，可以确保文本在传输过程中不受字符集影响被损坏，且接收方能够正确恢复原始的多语言文本。

import base64

# 多语言文本
text = "Hello, 世界"

# UTF-8 编码
binary_data = text.encode('utf-8')

# Base64 编码
encoded_data = base64.b64encode(binary_data)
print(encoded_data)  # Base64 编码后的文本

# 发送电子邮件（省略具体实现）

# 接收后解码
decoded_data = base64.b64decode(encoded_data)

# UTF-8 解码
original_text = decoded_data.decode('utf-8')
print(original_text)  # 输出: Hello, 世界

颜色编码¶

RGB¶

RGB 颜色模型的原理是基于光的加色混合（发射光）而不是颜料的减色混合（反射光）

三种基本颜色：红色（Red）、绿色（Green）和蓝色（Blue）

每种颜色的强度范围从 0 到 255，表示这三种基本颜色的混合比例，0 表示光的强度最低（没有光），255 表示光的强度最高。

background-color: rgb(255, 0, 0);

rgb(255, 0, 0)  /* 纯红色 */
rgb(0, 255, 0)  /* 纯绿色 */
rgb(0, 0, 255)  /* 纯蓝色 */
rgb(0, 0, 0)  /* 黑色，因为没有任何光 */
rgb(255, 255, 255)  /* 白色 */

RGBA¶

在 RGB 的基础上加了透明度（Alpha）

HEX¶

每两个字符表示红、绿、蓝的强度。

background-color: #FF0000;  /* 红色背景 */

HSL¶

使用色相、饱和度、亮度表示颜色。

background-color: hsl(0, 100%, 50%);  /* 红色背景 */